Stability of Ship. Ship stability is an area of naval architecture and ship design that deals with how a ship behaves at sea, both in still water and in waves, whether intact or damaged
Stable A ship is in a stable condition of stability if, when heeled
by an external force in still water to a small angle of inclination, it returns
to the upright when the force is removed.
Unstable condition : a
state of equilibrium of a body (as a pendulum standing directly upward from its
point of support) such that when the body is slightly displaced it departs
further from the original position — compare stable equilibrium.
Neutral equilibrium condition :
A ship is in a neutral condition of
stability if, when heeled by an external force in still water to a small angle
of inclination, it comes to rest at an indeterminate angle of heel within small
angles of inclination.
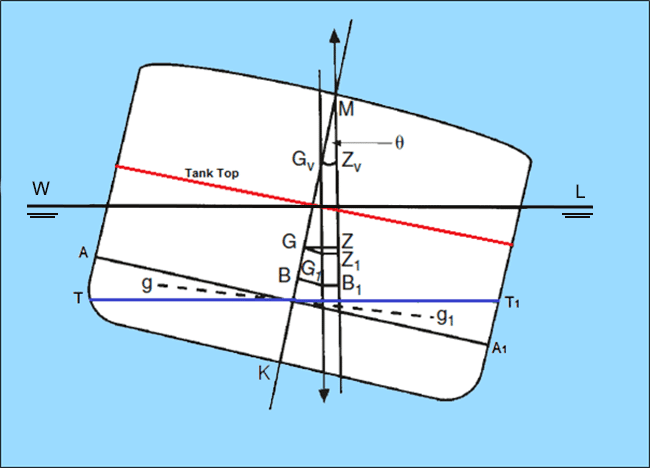
Righting Lever : The vessel's centre of gravity (G) has a
distinct effect on the righting lever (GZ) and consequently the ability of a
vessel to return to the upright position. The lower the centre of gravity (G),
the bigger is the righting lever (GZ).
Righting Moment. : A moment that tends to restore an
airplane or a naval vessel to its previous attitude after any small rotational
displacement called also restoring moment.
Metacenter - (shipbuilding)
the point of intersection
between two vertical
lines, one line
through the center
of buoyancy of the hull of a ship in equilibrium
and the other
line through the
center of buoyancy of the hull when the ship is inclined
to one side; the
distance of this intersection
above the center
of gravity is an indication of the stability of the
ship.
,
Metacentric Height (GM): Is a measurement of the initial static
stability of a floating body. It is calculated as the distance between the
centre of gravity of a ship and
its metacentre. A larger metacentric
height implies greater initial stability against overturning.
Centre Of Gravity (Cg): The centre of gravity of an object is the point at which the
whole weight of the object may be regarded as acting . if the object is
suspended from this point , then it will remain balanced and will not tilt
Curve of stability:
STABILITY AT LARGE ANGLES OF HEEL
When a ship
heels to an angle greater than about 10°, the principles on which the initial
stability were based are no longer true. The proof of the formula for BM was based on
the assumption that the two water planes intersect at the centerline and that
the wedges are right angled triangles. Neither of these assumptions may be made
for large angles of h«l and the stability of the ship must be determined from nest
principles.
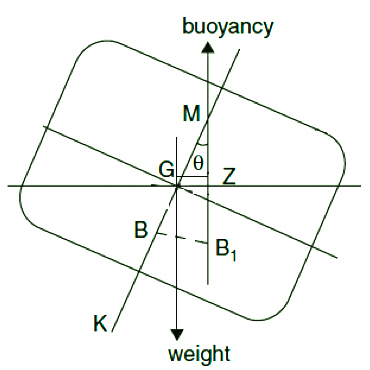
The righting
lever is the perpendicular distance from a vertical axis through the centre of
gravity G to the centre of buoyancy Bt . This distance may be found by
dividing the moment of buoyancy about this axis by the buoyancy. In practice
recourse is made to an instrument known as an integrator which may be used to determine the area of any plane and the moment of
the plane about a given axis. The method used is as
follows.
The amended righting levers are plotted
on a base of angle of heel to form tbe Curve of Statical Stability for the ship
in this condition of loading. The initial slope of the curve lies along a line drawn from the origin to Complotted vertically at one radian
(57.3·). The area under this curve to any given angle, multiplied by the gravitational
weight of the ship, is the work done in heeling
the ship to that angle
and is known as the Dynamical Stability.
Intact stability
For a cargo vessel, the intact stability requirements
are follows-
·
Initial GM or
meta centric height should not be less then 0.15 m.
·
Righting lever
GZ should be at least 0.2 m and angle of heel Ѳ ≥ 30̊.
·
Maximum
righting lever should occur at heel >30̊ preferably but
not less than 25̊.
·
The Area of the
GZ curve should be at least:
a)
0.055 m radian up to Ѳ = 30̊
b)
0.090 m radian up to Ѳ = 40̊
c)
0.03 m radian between 30̊ and 40̊ or between 30̊ and angle of down
flooding.




No comments:
Post a Comment